1 Answer

Ackim · Answer 1 · 2023-05-25T03:32:53+0000

It should be noted that the diagonals of a rectangle bisect each other and the diagonals are equal

From the given, the diagonals of the rectangle QUVX are QV and UX

Given

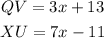
$\begin{gathered} QV=3x+13 \\ XU=7x-11 \end{gathered}$

Since the diagonals are equal, then

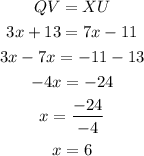
$\begin{gathered} QV=XU \\ 3x+13=7x-11 \\ 3x-7x=-11-13 \\ -4x=-24 \\ x=(-24)/(-4) \\ x=6 \end{gathered}$

Also, note that all angles in a rectangle are 90 degrees. Then

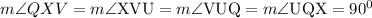
$m\angle QXV=m\angle\text{XVU}=m\angle\text{VUQ}=m\angle\text{UQX}=90^0$

Given

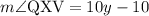
$m\angle\text{QXV}=10y-10$

So,

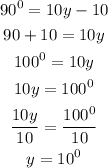
$\begin{gathered} 90^0=10y-10 \\ 90+10=10y \\ 100^0=10y \\ 10y=100^0 \\ (10y)/(10)=(100^0)/(10) \\ y=10^0 \end{gathered}$

Hence, x = 6

y= 10⁰

Please log in or register to add a comment.