Question

If you leave $5200 in an account earning 5% interest, compounded daily, how much money will be in the account after 2 years? (Round your answer to two decimal places.)

Answer 1

To solve this question, we just need to apply the compound interest formula.

The compound interest formula is

`A=P(1+(r)/(n))^(nt)`

Where A represents the final Amount, P represents the principal(starting amount), r the interest rate(written in decimals), n the number of times the interest is compounded per unit 't', and t represents the time.

Then, from the text we have

`\begin{gathered} P=5200 \\ r=0.05 \\ n=365 \\ t=2 \end{gathered}`

n is equal to 365 because we have 365 days in a year.

Plugging those values in our formula, we have

`A=5200(1+(0.05)/(365))^(365\cdot2)`

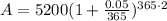
Now, we just need to calculate this value.

`\begin{gathered} A=5200(1+(0.05)/(365))^(365\cdot2) \\ A=5746.84941547\ldots\approx5746.85 \end{gathered}`

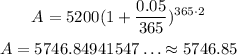
The amount of money in the account after 2 years will be $5746.85.