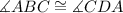Answer: 1.
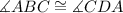
Step by step solution:
In a parallelogram, the opposite sides are parallel and equal. Not all his sides are equal just opposite sides.
In a Rhombus, all sides are equal and the opposite sides are parallel.
The above figure is a rhombus ABCD.
Now we know that the ABCD parallelogram is a rhombus if: Angle ABC is congruent (equal) to angle CDA