The area of the shared region between the curves
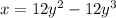 and
and
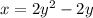 from
from
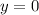 to
to
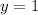 is approximately \( 1.33 \) square units when rounded to the nearest hundredth.
is approximately \( 1.33 \) square units when rounded to the nearest hundredth.
To find the area of the shared region analytically between the curves
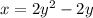 and
and
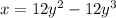 , we will need to set up an integral with the proper bounds.
, we will need to set up an integral with the proper bounds.
The shared region looks to be bound between
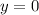 and
and
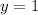 . We will integrate with respect to
. We will integrate with respect to
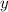 , subtracting the left curve from the right curve to get the area between them.
, subtracting the left curve from the right curve to get the area between them.
The integral to find the area
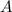 of the shared region is:
of the shared region is:
![\[ A = \int_(0)^(1) [(12y^2 - 12y^3) - (2y^2 - 2y)] \, dy \]](https://img.qammunity.org/2023/formulas/mathematics/college/dssijada0vok93n94xr9aarwehkse4y6xo.png)
Let's perform this integral step-by-step.
The area of the shared region between the curves
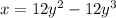 and
and
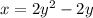 from
from
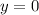 to
to
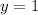 is approximately
is approximately
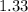 square units when rounded to the nearest hundredth.
square units when rounded to the nearest hundredth.