The probability that a student in the senior class had a part-time job is
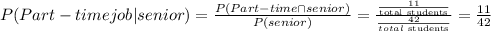
Whereas the probability that a student in the freshman class had a part-time job is
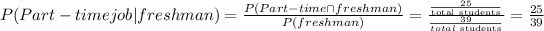
Notice that 11/42<25/39; thus, the answer is 'A senior is less likely than a freshman to have a job'