Question

Find the mean, median, and mode(s) of the data with and without the outlier. Describe the effect of the outlier on the measures of center.3.) 4, 15, 6, 12, 68, 124.) 0, 54, 62, 64, 55, 5, 54, 62

Answer 1

Given: Sets of data below

`\begin{gathered} data1:4,15,6,12,68,12 \\ data2:0,54,62,64,55,5,54,62 \end{gathered}`

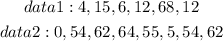
To Determine: The mean, median and mode

Solution

Data1; Calculate the mean as below

`\begin{gathered} Mean=(\Sigma x)/(n) \\ Mean=(4+15+6+12+68+12)/(6) \\ Mean=(117)/(6)=19.5 \end{gathered}`

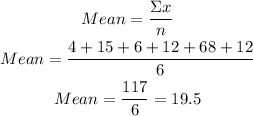
Calculate the median

`\begin{gathered} Re-arrange\text{ the data} \\ 4,6,12,12,15,68 \end{gathered}`

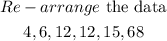
The middle numbers are

`12,12`

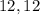
The average of the two middle numbers is

`\begin{gathered} Median=(12+12)/(2) \\ Median=(24)/(2) \\ Median=12 \end{gathered}`

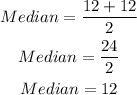
The mode is the number that occur the most

From the data 1 given, all the number appeared once except for 12 that appeared twice. Hence, the mode is 12

Data 2:

The mean is as calculated below

`Mean=(0+54+62+64+55+5+54+62)/(8)`
`\begin{gathered} Mean=(356)/(8) \\ Mean=44.5 \end{gathered}`

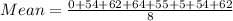
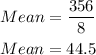
Calculate the median as shown below

`\begin{gathered} Re-arrange \\ 0,5,54,54,55,62,62,64 \end{gathered}`

The middle numbers are

`54,55`

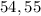
The median is the average of the two middle numbers

`Median=(54+55)/(2)=(109)/(2)=54.5`

Calculate the mode

It can be observed that 54 and 62 both appeared twice while other numbers appeared once. The mode is 54 and 62

Hence, the data is bi-modal, that it has two modes, 54 and 62

Let us calculate without outliers

Data 1

The outlier in data 1 is 68

`\begin{gathered} Mean=(4+6+12+12+15)/(5) \\ Mean=(49)/(5) \\ Mean=9.8 \end{gathered}`
`\begin{gathered} Re-arrange \\ 4,6,12,12,15 \\ Median=12 \\ Mode=12 \end{gathered}`

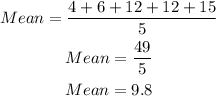
Data 2

The outliers are 0 and 5

`\begin{gathered} Mean=(54+54+55+62+62+64)/(6) \\ Mean=(351)/(6) \\ Mean=58.5 \end{gathered}`
`\begin{gathered} Re-arrange \\ 54,54,55,62,62,64 \\ Median=(55+62)/(2)=58.5 \\ Mode=54,and,62 \end{gathered}`

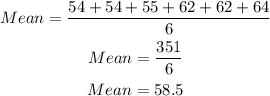
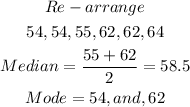
The outliers had major effect on the mean compare to the median and the mode