Question

Create the equation of a hyperbola centered at the origin, with a horizontal transverse axis, vertex at (–7, 0), and asymptotes of y equals plus or minus six sevenths x period Show your work. (4 points)

Answer 1

So,

First, remember that the general equation of a hyperbola is given by the following:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

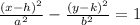
In our problem, we're given that this hyperbola is centered at the origin, so C(h,k) = C(0,0). Then, h=0, and k=0.

Our equation can be written as:

`(x^2)/(a^2)-(y^2)/(b^2)=1`

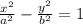
The vertex of this hyperbola is set in the point (-7,0). We could use the following equation to find the value of a:

`V=(h\pm a,k)`

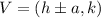
Where V is the vertex.

If we replace our values:

`(0\pm a,0)=(-7,0)`

So,

`a=\pm7`

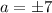
Since "a" is squared in the equation, it doesn't matter if it is -7 or 7. The +/- sign indicates that there are two vertices at (-7,0) and (7,0) respectively.

Now, to find b, we could use the fact that the asymptotes of the hyperbola are:

`y=\pm(6)/(7)`

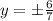
Remember that these asymptotes have the form:

`y=\pm(b)/(a)`

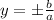
So, if we compare:

`\begin{gathered} a=\pm7 \\ b=\pm6 \end{gathered}`

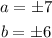
And, our equation will be:

`(x^2)/(49)-(y^2)/(36)=1`