Since the equation of the parabola is in standard form, then the x-coordinate of the vertex can be found like this:
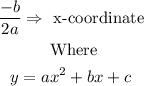
In this case, you have
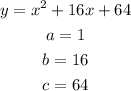
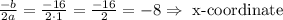
Now that you have the x coordinate of the vertex, you can replace this value into the original equation of the parabola to find the y coordinate of the vertex:
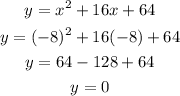
Therefore, the vertex of this parable is (-8,0).