Interest rate of the account is 4%
Step-by-step explanation:
initial amount = $3313
time = 20 years
Balance = future value = $7373.22
rate = ?
n = number of times compounded
n = continuously
The formula for continuous compounding:
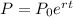

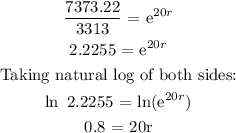

Interest rate of the account is 4%