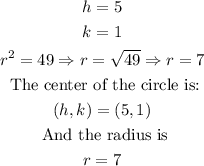Question

Find the center and radius of each circle x^2+y^2-10x-2y=23

Answer 1

The given equation is written in the general form of the equation of a circle:

`x^2+y^2-10x-2y=23`

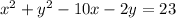
To find the center and radius, we need to write the equation in the standard form:

`(x-h)^2+(y-k)^2=r^2`

Where (h,k) are the coordinates of the center and r is the radius.

The first step is to complete the perfect square trinomials:

`(x^2-10x+a^2)+(y^2-2y+b^2)=23+a^2+b^2`

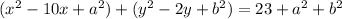
Where a and b are the numbers we need to find to complete the perfect square trinomials, so:

`\begin{gathered} x^2-10x+a^2=x^2-2*x*a+a^2=(x-a)^2 \\ \Rightarrow-10x=-2x*a\text{ Simplify x on both sides} \\ \Rightarrow-10=-2a\text{ Divide both sides by -2:} \\ \Rightarrow5=a \\ \Rightarrow(x-5)^2=x^2-10x+(-5)^2=x^2-10x+25 \end{gathered}`

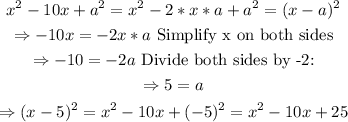
Apply the same procedure for the next perfect square:

`\begin{gathered} y^2-2y+b^2=y^2-2*y*b+b^2=(y-b)^2 \\ \Rightarrow-2y=-2yb\text{ Divide both sides by -2y} \\ \Rightarrow1=b \\ \Rightarrow(y-1)^2=y^2-2y+(1)^2=y^2-2y+1 \end{gathered}`

Now, we know a=5 and b=1, let's rewrite the equation:

`\begin{gathered} (x-5)^2+(y-1)^2=23+5^2+1^2 \\ (x-5)^2+(y-1)^2=23+25+1 \\ (x-5)^2+(y-1)^2=49 \end{gathered}`

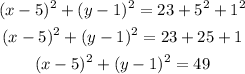
This equation is in the standard form, so:

`\begin{gathered} h=5 \\ k=1 \\ r^2=49\Rightarrow r=√(49)\Rightarrow r=7 \\ \text{ The center of the circle is:} \\ (h,k)=(5,1) \\ \text{ And the radius is} \\ r=7 \end{gathered}`