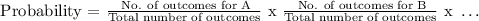A regular die has six sides with numbers 1 up to 6.
Thus, there are 3 even numbers in the die which are 2, 4 and 6.
And there is only one side of the die that has the number 3.
This means that we are looking for 4 possibilities in rolling a die.
Computing the probability, we get:
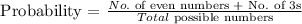
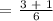
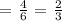
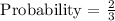
Therefore, the probability of getting a 3 or even number is 2/3.
Note:
For "or" scenario, the following equation must be applied:
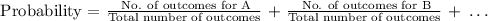
For "and" scenario, the following equation must be applied: