ANSWER
23.6 centimeters
Step-by-step explanation
The height of the candle is a linear function of time it has been burning.
A linear function is generally represented as:
y = mx + c
where m = slope
c = y intercept
From the equation:
y = height of candle
x = time it has been burning
After 5 hours, it's height was 24.5 cm
After 18 hours, it's height is 20.6 cm
We have to find the function that represents the height of the candle.
We will first find the slope and then use formula:

Find the slope by using formula:
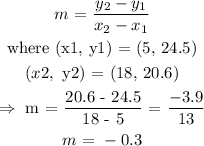
Now, find the function:
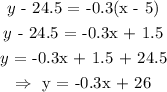
Now, to find the height of the candle after 8 hours, we will make x = 8 and then find y:
y = -0.3(8) + 26
y = -2.4 + 26
y = 23.6 centimeters
That is the height of the candle after 8 hours.