Question

Researchers in Antarctica discovered a warm sea current under a glacier that is causing the glacier to melt. The ice shelf of the glacier had a thickness of approximately 625 m when it was first discovered. The thickness of the ice shelf is decreasing at an average rate of 0.72 m per day. Which function can be used to find the thickness of the ice shelf in meters x days since the discovery?A: t(x)=0.72(x+625)B: t(x)=625-0.72xC: t(x)= - 0.72(x+625)D: t(x)= 625 + 0.72x

Answer 1

We define the following variables:

• t(x) = thickness of the ice in terms of x,

,

• x = days since the discovery.

From the statement of the problem we know that:

• the thickness on the day of the discovery (x = 0) was t = 625,

,

• the thickness is decreasing at an average rate of 0.72 m per day.

Because the thickness is decreasing the same thickness each day, the problem can be described by a linear function:

`t(x)=m\cdot x+b,`

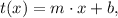
where:

• b is the value of t when x = 0, i.e b = 625,

,

• and m is the rate of change of the thickness, m = -0.72.

Replacing the values of m and b in the equation above we get:

`t(x)=-0.72x+625=625-0.72x\text{.}`

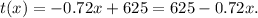
Answer

B: t(x)=625-0.72x