Question

It's 119 miles from Ayville to Beeville. It's another 90 miles from Beeville to Charlwoods. Russell drives 10 miles faster from Beeville to Charlwoods than from Ayville to Beeville. If his combined travel time is 5.4 hours, what are his average speeds?

Answer 1

Let v be the average speed from Ayville to Beeville.

Let t_1 be the time that Russell took to travel from Ayville to Beevile, and t_2 the time that he took to travel from Beeville to Charlwoods.

Remember the formula that relates the average speed of a moving object with the distance that it traveled and the time that it takes to travel that distance:

`v=(d)/(t)`

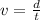
Isolate t from the equation:

`t=(d)/(v)`

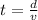
For the first part of the journey, the distance from Ayville to Beeville is 119 miles. Then:

`t_1=(119mi)/(v)`

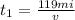
For the second part of the journey, the distance from Beeville to Charlwoods is 90 miles, and Russell drives 10 miles per hour faster. Then:

`t_2=(90mi)/(v+10(mi)/(h))`

Since the combined travel time is 5.4 hours, then:

`t_1+t_2=5.4h`

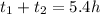
Substitute the expression for t_1 and t_2:

`\Rightarrow(119mi)/(v)+(90mi)/(v+10(mi)/(h))=5.4h`

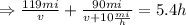
Add both fractions on the left member of the equation:

`\Rightarrow((119mi)(v+10\cdot(mi)/(h))+(90mi)(v))/((v)(v+10(mi)/(h)))=5.4h`

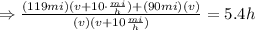
Simplify the expression on the numerator:

`\begin{gathered} \Rightarrow(119mi\cdot v+1190\cdot(mi^2)/(h)+90mi\cdot v)/((v)(v+10(mi)/(h)))=5.4h \\ \Rightarrow(209mi\cdot v+1190\cdot(mi^2)/(h))/((v)(v+10(mi)/(h)))=5.4h \end{gathered}`

Multiply the factors on the denominator:

`\Rightarrow(209mi\cdot v+1190\cdot(mi^2)/(h))/(v^2+10(mi)/(h)v)=5.4h`

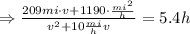
Multiply both sides of the equation by (v^2+10(mi/h)v):

`\begin{gathered} \Rightarrow209mi\cdot v+1190\cdot(mi^2)/(h)=(5.4h)(v^2+10(mi)/(h)v) \\ \Rightarrow209mi\cdot v+1190\cdot(mi^2)/(h)=5.4h\cdot v^2+54mi\cdot v \end{gathered}`

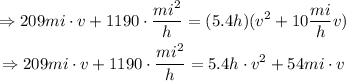
Notice that we obtained a quadratic equation for v. Write it in standard form and use the quadratic formula to find the values of v. Recall the following:

`\begin{gathered} ax^2+bx+c=0 \\ \Rightarrow x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

Then, from the equation for v:

`\begin{gathered} \Rightarrow209mi\cdot v+1190\cdot(mi^2)/(h)=5.4h\cdot v^2+54mi\cdot v \\ \Rightarrow0=5.4h\cdot v^2+54mi\cdot v-209mi\cdot v-1190\cdot(mi^2)/(h) \\ \Rightarrow5.4h\cdot v^2-155mi\cdot v-1190\cdot(mi^2)/(h)=0 \end{gathered}`

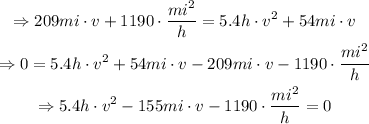
To use the quadratic formula, notice that a=5.4h, b=-155mi and c=-1190(mi^2/h):

`\begin{gathered} \Rightarrow v=\frac{-(-155mi)\pm\sqrt[]{(-155mi)^2-4(5.4h)(-1190\cdot(mi^2)/(h))}}{2(5.4h)} \\ =\frac{155mi\pm\sqrt[]{24,025mi^2+25,704mi^2}}{10.8h} \\ =(155mi\pm223mi)/(10.8h) \end{gathered}`

Using only the positive value for the speed, we get that:

`\begin{gathered} v=(155mi+223mi)/(10.8h) \\ =(378mi)/(10.8h) \\ =35(mi)/(h) \end{gathered}`

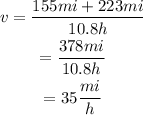
Since v is the speed from Ayville to Beevile and the speed from Beevile to Charlwoods is 10 miles per hour faster, then, the average speeds for each part, are:

From Ayville to Beevile: 35 miles per hour.

From Beevile to Charlwoods: 45 miles per hour.