1 Answer

Vangorra · Answer 1 · 2023-03-13T10:57:00+0000

Calculate the slope of the line joining the points (1,1) and (-3,-1).

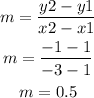
$\begin{gathered} m=(y2-y1)/(x2-x1) \\ m=(-1-1)/(-3-1) \\ m=0.5 \end{gathered}$

Use the equation m1m2=-1 to calculate the slope of the perpendicular line.

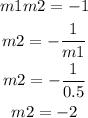
$\begin{gathered} m1m2=-1 \\ m2=-(1)/(m1) \\ m2=-(1)/(0.5) \\ m2=-2 \end{gathered}$

Given that, the line passes through the point (-3,4).

Use point slope form to calculate the equation of the line.

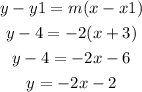
$\begin{gathered} y-y1=m(x-x1) \\ y-4=-2(x+3) \\ y-4=-2x-6 \\ y=-2x-2 \end{gathered}$

Therefore, the equation of the line is y=-2x-2.

Please log in or register to add a comment.