hello
the question given requests that we find a missing angle from a triangle
from the triangle above, we can simply use trigonometric ratios on this.
trigonometric ratios are SOHCAHTOA
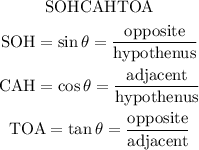
from the question given we have the value of opposite and adjacent and we can simply use tangent to find the missing angle

from the calculations above, the value of theta is equal to 50.6 degrees which corresponds to option B