Question

Solve the system of functions, y2 = 3x and y = 7x.

Answer 1

Step-by-step explanation

We have the following system of functions:

`\begin{gathered} y^2=3x \\ y=7x \end{gathered}`

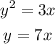
The second equation gives us an expression for y. We can replace y with these expression in the first equation:

`\begin{gathered} y^2=(7x)^2=3x \\ 7^2\cdot x^2=3x \\ 49x^2=3x \end{gathered}`

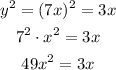
We can substract 3x from both sides:

`\begin{gathered} 49x^2-3x=3x-3x \\ 49x^2-3x=0 \end{gathered}`

The x is a factor of both terms on the left. Then we can rewrite this equation:

`\begin{gathered} 49x^(2)-3x=0 \\ x(49x-3)=0 \end{gathered}`

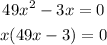
So we have that the product of two terms is equal to 0. This happens when any of them is equal to 0 so we have two equations:

`\begin{gathered} x=0 \\ 49x-3=0 \end{gathered}`

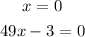
From the first we have x=0 and we can add 3 to both sides of the second equation:

`\begin{gathered} 49x-3+3=0+3 \\ 49x=3 \end{gathered}`

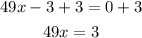
Then we divide both sides by 49:

`\begin{gathered} (49x)/(49)=(3)/(49) \\ x=(3)/(49) \end{gathered}`

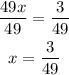
So we have the two x-values of the solutions: x=0 and x=3/49. In order to find their respective y-values we can use any of the two original functions:

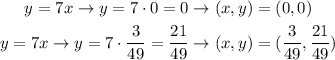
`\begin{gathered} y=7x\rightarrow y=7\cdot0=0\rightarrow(x,y)=(0,0) \\ y=7x\rightarrow y=7\cdot(3)/(49)=(21)/(49)\rightarrow(x,y)=((3)/(49),(21)/(49)) \end{gathered}`Answer

We have two solutions: (0,0) and (3/49,21/49). We can round the values of the second solution:

`\begin{gathered} (3)/(49)\cong0.06 \\ (21)/(49)\cong0.43 \end{gathered}`

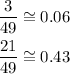
Then the solutions are (0,0) and (0.06,0.43). Then the answer is the fourth option.