Question

Help please thank you last tutor did not know how

Answer 1

Given:

Count in bacteria culture after 20 minutes = 200

Count in bacteria culture after 40 minutes = 1900

Required: Find the initial size, doubling period, population after 60 minutes and time at which the population will reach 11000

Explanation:

The exponential growth can be modeled by

`A=A_0e^(kt)`

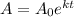
where A0 is the initial size and k is the growth rate.

Plug the condition A(20) = 200.

`\begin{gathered} 200=A_0e^(k\cdot20) \\ =A_0e^(20k) \end{gathered}`

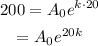
Plug the condition A(40) = 1900.

`\begin{gathered} 1900=A_0e^(k\cdot40) \\ =A_0e^(40k) \end{gathered}`

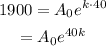
Divide both of them.

`\begin{gathered} (1900)/(200)=(A_0e^(40k))/(A_0e^(20k))=e^(20k) \\ 20k=\ln(9.5) \\ k=(\ln(9.5))/(20) \end{gathered}`

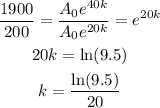
Thus,

`A=A_0e^{(\ln(9.5))/(20)t}`

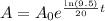
Substitute A(20) = 200 to find the initial count.

`\begin{gathered} 200=A_0e^{(\ln(9.5))/(20)\cdot20} \\ =9.5A_0 \\ A_0=(200)/(9.5)\approx21 \end{gathered}`

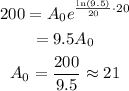
Thus,

`A=21e^{(\ln(9.5))/(20)t}`

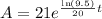
To find the doubling, find t at which A(t) = 42.

`\begin{gathered} 42=21e^{(ln(9.5))/(20)t} \\ 2=e^{(ln(9.5))/(20)t} \\ (\ln(9.5))/(20)t=\ln(2) \\ t=(\ln(2)\cdot20)/(\ln(9.5)) \\ =6.158 \end{gathered}`

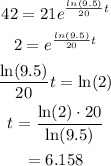
The doubling time is 6.158 minutes.

To find the population after 60 minutes, substitute 60 for t into A(t).

`\begin{gathered} A=21e^{(\ln(9.5))/(20)\cdot60} \\ \approx18005 \end{gathered}`

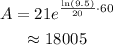
The count of bacteria after 60 minutes is 18005.

To find the time required for the culture of 11000, find t at which A(t) = 11000.

`\begin{gathered} 21e^{(\ln(9.5))/(20)t}=11000 \\ e^{(\ln(9.5))/(20)t}=523.81 \\ (\ln(9.5))/(20)t=6.261 \\ t=55.622 \end{gathered}`

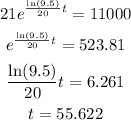
The count of bacteria will reach 11000 in 55.622 minutes.

Final Answer:

Initial count = 21

The doubling time is 6.158 minutes.

The count of bacteria after 60 minutes is 18005.

The count of bacteria will reach 11000 in 55.622 minutes.