Question

height in feet after t seconds is given by s(t) = - 1612 +48t. Find the number of seconds itIf an object is projected upward from ground level with an initial velocity of 48 ft per sec, thenwill take to reach its maximum height. What is this maximum height?The object will take second(s) to reach its maximum height(Simplify your answer)n begin Lessonaringn begin MathentsIn(0/1)B(0/1)12 (0/1)16 (0/1)20 (0/1)24 (0/1)5aryEnter your answer in the answer box and then click Check AnswerpartremainingClear All

Answer 1

Recall that the given function is a parabola. It looks something like this

The highest point of this parabola is the vertex. recall that the general equation of a parabola is of the form

`y\text{ =a}\cdot(x-h)^2+k`

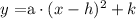
where h and k are the coordinates of the vertex. We are interested at the coordinate h. So what we will do is complete the square to get the general equation. So we start with

`\text{ -16t}^2+48t`

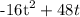
we factor out -16, so we get

`\text{ -16}\cdot(t^2\text{ -3t)}`

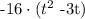
Now, note that

`t^2-3t+(9)/(4)=(t-(3)/(2))^2`

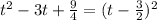
So this implies that

`t^(2)\text{ -3t = (t - }(3)/(2))^2\text{ -}(9)/(4)`

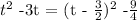
so we replace this value and we get

`\text{ -16}\cdot t^2+48t\text{ = -16}\cdot((t\text{ -}(3)/(2))^2\text{ -}(9)/(4))\text{ =-16}\cdot(t\text{ -}(3)/(2))^2+16\cdot(9)/(4)`

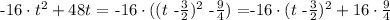
note that in this expression, the value of h would be 3/2. So the time it needs to reach its maximum height is 3/2 seconds. The highest point would be the value of k. So, in this case we have

`k=(16\cdot9)/(4)=9\cdot4=36`

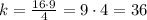
so the highest point is would be 36 meters.