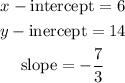Question

Find the slope x intercept and y intercept of the standard form equation below 7x + 3y equals 42

Answer 1

Given the equation of the line :

`7x+3y=42`

To find the slope, we will write the equation of the line in slope- intercept form

So, it will be as following :

`\begin{gathered} 7x+3y=42 \\ 3y=-7x+42 \end{gathered}`

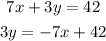
Divide all terms by 3

`\begin{gathered} (3y)/(3)=-(7x)/(3)+(42)/(3) \\ \\ y=-(7)/(3)x+14 \end{gathered}`

Which will be similar to the general form: y = m * x + b

Where m is the slope

So, the slope of the given equation = -7/3

To find y- intercept, substitute with x = 0

`\begin{gathered} 7\cdot0+3y=42 \\ 3y=42 \\ \\ y=(42)/(3)=14 \end{gathered}`

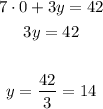
To find x- intercept , substitute with y = 0

`\begin{gathered} 7x+3\cdot0=42 \\ 7x=42 \\ \\ x=(42)/(7)=6 \end{gathered}`

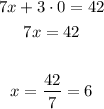
so, the answer is :

`\begin{gathered} x-\text{intercept}=6 \\ y-\text{inercept}=14 \\ \text{slope}=-(7)/(3) \end{gathered}`