Question

true or false?17. The focci of an ellipse are located at 1/3 the length of the major axis from both sides of the center.

Answer 1

To solve this problem and find if the statement is true, we can start by remembering the general equation for an ellipse:

`(x^2)/(a^2)+(y^2)/(b^2)=1`

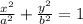
where a and b are the major axis and the minor axis for the ellipse, as shown in the following diagram:

The foci of an ellipse, are the focal points of the ellipse, for reference, we show them in the diagram:

The foci can be found using the following equation:

`f=\sqrt[]{a^2-b^2}`

To prove if the foci f is really 1/3 of the length of the major axis (in this case the major axis is a) we can give random values to a and b.

Values for a and b:

a=6

b=4

If the foci of the ellipse were located at 1/3 of the length of the major axis, we should find that the foci "f" is 1/3 of 6, thus, we should find that f=2, let's see if that is true by substituting a and b into the formula for f:

`f=\sqrt[]{a^2-b^2}`
`f=\sqrt[]{6^2-4^2^{}}`
`\begin{gathered} f=\sqrt[]{36-16} \\ f=\sqrt[]{20} \end{gathered}`

solving the square root we find the value of f:

`f=4.47`

Instead of 2 (which would have been 1/3 of the major axis), we find that f is 4.47, thus the statement "The foci of an ellipse are located at 1/3 the length of the major axis from both sides of the center." Is NOT TRUE.

Answer: False