Question

The volume of this triangular prism is 20,580 cubic millimeters. What is the value of p?

Answer 1

We have that the formula of the volume of the triangular prism is:

`V=A\cdot h`

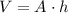
Where A is the area of the base and h is the height. Then we can write the volume like this:

`\begin{gathered} A=(p\cdot b)/(2) \\ \Rightarrow V=((p\cdot b)/(2))\cdot h=(p\cdot b\cdot h)/(2) \end{gathered}`

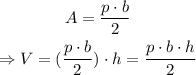
now, if b=20, h=42 and V=20580, then we substitute and solve for p:

`\begin{gathered} V=(p\cdot b\cdot h)/(2) \\ \Rightarrow20580=(p\cdot20\cdot42)/(2)=420\cdot p \\ \Rightarrow p=(20580)/(420)=49 \\ p=49 \end{gathered}`

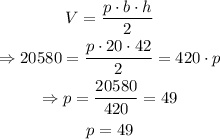
therefore, the value of p is 49 milimeters