Question

Jackie had 2 part time jobs at Shoney's Restaurant. One week she earned a total $306, working 12 hours as a cashier and 10 hours as a cook. The next week, sheworked 14 hours as a cashier and 22 hours as a cook, earning $512. How much doesshe earn per hour as a cashier?

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Represent the terms with a variable

Let x be the amount she earns per hour as a cashier

Let y be the amount she earns per hour as a cook

STEP 2: Interpret the statements in the question as seen below:

`\begin{gathered} 12x+10y=306 \\ 14x+22y=512 \end{gathered}`

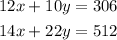
STEP 3: Solve the simultaneous equation using elimination to get x and y

`\begin{gathered} 12x+10y=306---(1) \\ 14x+22y=512----(2) \\ \\ \text{ Multiply equation 1 by 14 and equation 2 by 12} \\ 14\lbrack12x+10y=306\rbrack\Rightarrow168x+140y=4284----(3) \\ 12\lbrack14x+22y=512\Rightarrow168x+264y=6144----(4) \\ \\ \text{Subtract equation 4 from equation 3} \\ 168x\text{ cancels 168x, we have;} \\ 140y-264y=4284-6144 \\ -124y=-1860 \\ \text{Divide both sides by -124} \\ (-124y)/(-124)=(-18600)/(-124) \\ y=15 \end{gathered}`

STEP 4: Solve any of equation to get the value of x

`\begin{gathered} \text{From equation 1} \\ 12x+10y=306 \\ y=15\text{, By substitution;} \\ 12x+10(15)=306 \\ 12x+150=306 \\ \text{Subtract 150 from both sides} \\ 12x+150-150=306-150 \\ 12x=156 \\ \text{Divide both sides by 12} \\ (12x)/(12)=(156)/(12) \\ x=13 \end{gathered}`

Since x represents the amount she earns as a cashier, hence She earns $13 per hour as a cashier