Triangle ABC
A(4,-2)
B(5,5)
C(-1,3)
To calculate each side length you have to apply the Pythagoras theorem:

Considering each side of the triangle as the hypothenuse of a rigth triangle you can say that their base and heigth will be determined by their coordinates over the x and y axis so that:
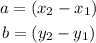
Then:
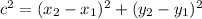
Finally:
![c=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/4fja8fmk57idw9ue8sego807121yqc9eis.png)
Side AB
c=AB
A(4,-2) B(5,5)
![\begin{gathered} AB^{}=\sqrt[]{(5-4)^2+(5-(-2))^2} \\ AB=5\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1phg8zqxm8zzkr8h86rnqpybafhq72zp49.png)
Side BC
c=BC
B(5,5) C(-1,3)
![\begin{gathered} BC=\sqrt[]{(5-(-1))^2+(5-3)^2} \\ BC=2\sqrt[]{10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qhk10opnx1uojcyh67o0dpcc8alk2k00mk.png)
Side AC
c= AC
A(4,-2) C(-1,3)
![\begin{gathered} AC=\sqrt[]{(4-(-1))^2+(-2-3)^2} \\ AC=5\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/e2p067tdnrixld7d73tvrkdei9bkktn0no.png)
Acording to the calculated lengths AB≅AC
The correct option is a)