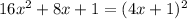Factoring a trinomial
In the following trinomial
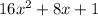
We find the first and second terms can be written
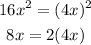
Since the perfect square trinomial is given by the equation
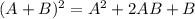
If we replace A = 4x and B = 1, then, the last equation is
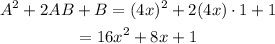
Then, we can factor the given trinomial using the perfect square trinomial equation: