We have that the formula of the volume of a Sphere is
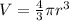
a.
the radius of the sphere is r=2
the volume will be
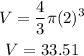
b.
the radius of the sphere is r=4
the volume will be
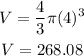
c. as we can see the radius of the sphere b, is twice the radius of sphere a, but as we can see because we calculated the volume of spheres, the volume of the sphere b is much bigger than the twice of the volume of the sphere a. It is because we don't have a linear relationship because we have an exponent 3 in the radius in the formula of the volume