First, write an equation for the amount of money he wins for each plan, given a time of h hours:
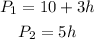
If both plans cost the same amount, then P_1 = P_2, therefore:
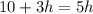
Solve the equation for h:
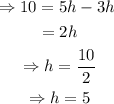
Therefore, for Part A the equation is 10+3h=5h
For Part B, the value of h when both plans cost the same amount is h=5.