Question

Roxie is a show dog. Her trainer wants her to have a beautiful and brilliant coat. The veterinarian suggested a special diet for the trainer to follow. Each feeding Roxie eats 2/3 of a can of wet dog food, 1/8 of a bag of dry dog food, and 3/5 of a patty of special meat. The special meat comes in packages of 6 patties. Roxie has two meals per day. The dog is completely out of food. The trainer goes to the store and buys 24 cans of wet dog food, 4 bags of dry dog food, and 3 packages of meat. How many days will the dog be fed before the trainer needs to buy any more food? Which type of dog food wil the trainer run out of first? How much of the other two types of dog food will be left after the first type of dog food runs out?

Answer 1

For each feeding, the proportion of food eaten by Roxie is:

• Wet dog food = 2/3 of a can

,

• Dry dog food =1/8 of a bag

,

• Special meat = 3/5 of a patty

The trainer goes to the store and buys 24 cans of wet dog food, 4 bags of dry dog food, and 3 packages of meat.

Since there are 6 patties in 1 package, the number of patties bought by the trainer = 3 X 6 = 18 Patties

Since the dog is fed twice a day, the dog eats the following per day:

`\begin{gathered} \text{Wet dog food}=(2)/(3)*2=(4)/(3)\text{ of a can} \\ \text{Dry dog food}=(1)/(8)*2=(1)/(4)\text{ of a bag} \\ \text{Special meat}=(3)/(5)*2=(6)/(5)\text{ of a patty} \end{gathered}`

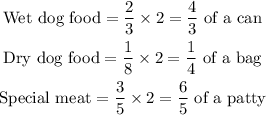
Therefore, the number of days that each food type bought will last will be:

`\begin{gathered} Wet\; dog\; food\; \colon24/(4)/(3)=18\; days\text{ } \\ Dry\; dog\; food\; \colon4/(1)/(4)=16\; days\text{ } \\ Special\; meat\; \colon18/(6)/(5)=15\; days \end{gathered}`

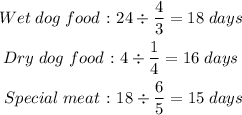
(a)The dog will be fed for 15 days before the trainer needs to buy more food.

(b)The trainer will run out of the special meat first.

Since the dogs will be fed for 15 days, the amount of the other two types of dog food will be left after the first type of dog food runs out will be:

`\begin{gathered} \text{Wet dog food} \\ 24-(15*(4)/(3))=4\text{ cans} \\ Dry\text{ dog food} \\ 4-(15*(1)/(4))=0.25\text{ of a bag} \end{gathered}`

(c)Therefore:

• 4 cans of the wet dog food will remain; and

,

• 0.25 of a bag of the dry dog food will remain.