The sum of the interior angles of a polygon is given by:
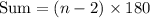
Where n is the number of sides.
When we divide the sum by the number of sides we obtain the measure of each interior angle, then:
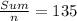
By replacing the sum by the formula we can solve for n:

Thus, the number of sides of the regular polygon is 8.