Question

Consider the following table with information about a sample of students from Phoenix HighSchool and where they live. If a person is randomly selected determine the following probability:P(Female or Suwanee).

Answer 1

Given:

Total persons, n(S)=80.

Let P(A) be the probability of selecting a person from females.

Let P(B) be the probability of selecting a person from suwanee.

From the table value,

We have,

`\begin{gathered} n(A)=30 \\ n(B)=24 \\ n(A\cap B)=8 \end{gathered}`

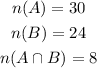
To determine the probability P(Female or Suwanee):

We know that the formula,

`P(A\cup B)=P(A)+P(B)-P(A\cap B)`

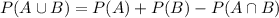
Find P(A), P(B) and P(A and B):

`\begin{gathered} P(A)=(n(A))/(n(s)) \\ =(30)/(80) \end{gathered}`
`\begin{gathered} P(B)=(n(B))/(n(s)) \\ =(24)/(80) \end{gathered}`

`\begin{gathered} P(A\cap B)=(n(A\cap B))/(n(s)) \\ =(8)/(80) \end{gathered}`

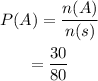
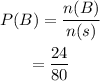
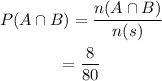
Hence, using the formula we get,

`\begin{gathered} P\mleft(Female(or)Suwanee\mright)=(30)/(80)+(24)/(80)-(8)/(80)_{} \\ =(46)/(80) \\ =(23)/(40) \end{gathered}`

Hence, the probabaility of selecting a person either female or suwanee is,

`(23)/(40)`

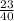
Therefore, the correct option is A.