We are asked to complete each table converting the given measure to its equivalent measure in degrees or radians
Degrees to Radians:
We use the following relation to convert from degrees to radians
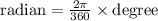
Radians to Degrees:
We use the following relation to convert from radians to degrees
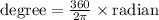
Now let us perform the conversions
Table 1:
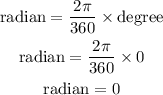
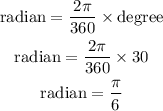
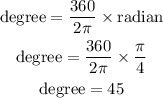
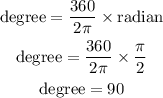
Table 2:
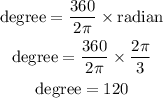
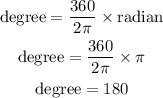
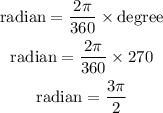
Therefore, both the tables have been completed with degrees and radians values.