a. To find (fog)(x), evaluate f(x) at x=g(x), this is, replace each x in f(x) for g(x):

b. Follow the same procedure for (gof)(x):
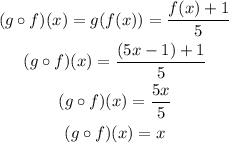
c. Evaluate the obtained expression at x=-1:
(fog)(x)=x
(fog)(-1)=-1
d. Evaluate the obtained expression at x=-1:
(gof)(x)=x
(gof)(-1)=-1