Question

Let f(x) = 5x – 1 and g(x)= x+1/5, find:a. (f °g)(x) =b. (g ° f)(x)=c. (fog)( - 1) =d. (gof)( - 1) =

Answer 1

a. To find (fog)(x), evaluate f(x) at x=g(x), this is, replace each x in f(x) for g(x):

`\begin{gathered} (f\circ g)(x)=f(g(x))=5(g(x))-1 \\ (f\circ g)(x)=5((x+1)/(5))-1 \\ (f\circ g)(x)=x+1-1 \\ (f\circ g)(x)=x \end{gathered}`

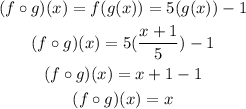
b. Follow the same procedure for (gof)(x):

`\begin{gathered} (g\circ f)(x)=g(f(x))=(f(x)+1)/(5) \\ (g\circ f)(x)=((5x-1)+1)/(5) \\ (g\circ f)(x)=(5x)/(5) \\ (g\circ f)(x)=x \end{gathered}`

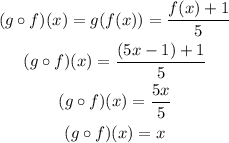
c. Evaluate the obtained expression at x=-1:

(fog)(x)=x

(fog)(-1)=-1

d. Evaluate the obtained expression at x=-1:

(gof)(x)=x

(gof)(-1)=-1