Question

List the first 9 terms of the sequence defined recursively by Sn = Sn-2. (Sn-1 - 1), with S1 = 2 and

S2 = 3
Looking for help wit question 2.

Answer 1

• (1)2, 3, 4, 9, 32, 279, 8896, 241,705, and 22,077,238,784

,

• (2)2,490,930

• (3)Neither

Explanation:

Given a sequence defined recursively as follows:

`\begin{gathered} s_n=s_(n-2)\cdot\left(s_(n-1)-1\right) \\ \begin{equation*} s_1=2 \end{equation*} \\ s_2=3 \end{gathered}`

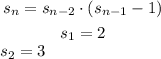
Part 1

First, we find the first 9 terms of the sequence.

`\begin{gathered} s_3=s_(3-2)(s_(3-1)-1)=s_1(s_2-1)=2(3-1)=2*2=4 \\ s_4=s_(4-2)(s_(4-1)-1)=s_2(s_3-1)=3(4-1)=3*3=9 \\ s_5=s_(5-2)(s_(5-1)-1)=s_3(s_4-1)=4(9-1)=4*8=32 \\ s_6=s_(6-2)(s_(6-1)-1)=s_4(s_5-1)=9(32-1)=9*31=279 \end{gathered}`
`\begin{gathered} s_7=s_(7-2)(s_(7-1)-1)=s_5(s_6-1)=32(279-1)=32*278=8896 \\ s_8=s_(8-2)(s_(8-1)-1)=s_6(s_7-1)=279(8896-1)=2,481,705 \\ s_9=s_(9-2)(s_(9-1)-1)=s_7(s_8-1)=8896(2,481,705-1)=22,077,238,784 \end{gathered}`

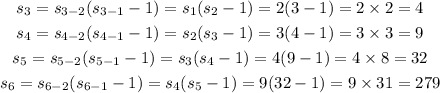
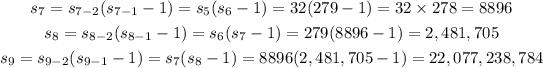
The first 9 terms of the sequence are:

`2,3,4,9,32,279,8896,241,705,\text{ and }22,077,238,784`

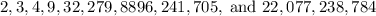
Part 2

Next, find the sum of the first 8 terms:

`\begin{gathered} \sum_(k=1)^8S_k=s_1+s_2+\cdots+s_8 \\ =2+3+4+9+32+279+8896+2481705 \\ =2,490,930 \end{gathered}`

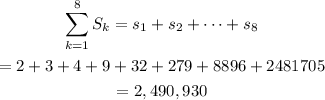
The sum of the first 8 terms of the sequence is 2,490,930.

Part 3

The sequence is neither arithmetic nor geometric.