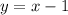Question

Line Equation from Two PointsSep 22,5:09:53 PMWatch help videonoWhat is an equation of the line that passes through the points (7,6) and(-2, -3)?Answer:Submit Answerattempt 1 out of 2

Answer 1

We must find an equation for the line that passes through the points:

• A = (xA,yA) = (7,6),

,

• B = (xB,yB) = (-2,-3).

The general slope-intercept equation of a line is:

`y=m\cdot x+b,`

where m is the slope and b is the y-intercept of the line.

1) We can compute the slope m with the coordinates of two points of the line and the following formula:

`m=\frac{y_B-y_A}{x_B-x_A_{}},`

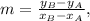
where (xA,yA) and (xB,yB) are the coordinates of the points A and B, respectively.

Replacing the coordinates of the points in the formula above, we get:

`m=(-3-6)/(-2-7)=1.`

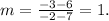
2) To find the y-intercept b we replace the coordinate of one of the points (A for example) and the value of m = 1 in the general equation of the line, and then we solve for b:

`\begin{gathered} y_A=m\cdot x_A+b, \\ 6=1\cdot7+b, \\ b=6-7, \\ b=-1. \end{gathered}`

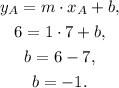
Using the values m = 1 and b = -1, we find that the equation of the line is:

`y=x-1`

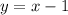
Answer

The equation of the line is

`y=x-1`