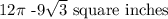Question

Please help me find the area of the shaded sector or segment.

Answer 1

Given:

To evaluate the area of the shaded portion, we subtract the area of the triangle OAB from the area of the sector of the circle.

Thus,

Step 1: Evaluate the area of the sector of the circle.

The area of the sector of a circle is expressed as

`\begin{gathered} Area_(sector)=(\theta)/(360)*\pi r^2 \\ where \\ \theta\Rightarrow central\text{ angle of the sector} \\ r\Rightarrow radius\text{ of the circle} \end{gathered}`

Thus,

`\begin{gathered} \theta=180-(30+30)=180-60=120 \\ r=6\text{ in.} \\ thus, \\ Area_(sector)=(120)/(360)*\pi*6\text{ in}*6\text{ in} \\ =12\pi\text{ square inches} \end{gathered}`

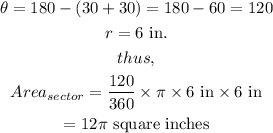
Step 2: Evaluate the area of the triangle OAB.

The area of the triangle is evaluated as

`\begin{gathered} Area_(triangle)=(1)/(2)ab\sin C \\ where \\ a\Rightarrow OA \\ b=OB \\ C\Rightarrow\angle O \end{gathered}`

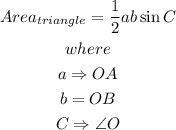
Thus, we have

`\begin{gathered} OA=OB=6\text{ in.} \\ \angle O=120 \\ Thus, \\ Area_(triangle)=(1)/(2)*6\text{ in}*6\text{ in}*\sin120 \\ =9√(3)\text{ square inches} \end{gathered}`

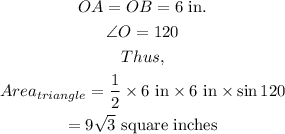
Step 3: Evaluate the area of the shaded region.

Thus, we have

`\begin{gathered} Area\text{ of shaded region = area of sector - area of triangle} \\ =12\pi\text{ -9}√(3) \\ \end{gathered}`

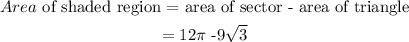
Hence, the area of the shaded portion is

`12\pi\text{ -9}√(3)\text{ square inches}`