Question

Find the area of the following shape. Be sure to show all of your work.

Answer 1

54

1) Examining that shape, we can see that there is a triangle and a quadrilateral making up that shape.

2) Let's write down the coordinates of each vertex:

A(5,6)

B(11, 3)

C (11,-3)

D (4, -3)

E (5,3)

F (1,3)

2.2) Since this is an irregular polygon, then we can use the Gauss formula(a.ka. Shoelace formula) to find the Area writing matrices:

`\begin{gathered} \begin{bmatrix}5 & 6 \\ 11 & 3 \\ 11 & -3 \\ 4 & -3 \\ 5 & 3 \\ 1 & 3 \\ 5 & 6\end{bmatrix} \\ \end{gathered}`

Notice that we have repeated x_1 and y_1 in the last row. We can make our "shoelace" by multiplying the diagonals this way:

`\begin{gathered} A_1=(1)/(2)|(15-33-33+12+15+6)-(66+33-12-15+3+15)| \\ A=54 \end{gathered}`

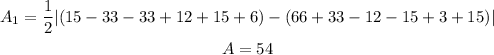
2.4) Now, we can calculate the absolute difference between these two products:

And finally, multiply by 1/2 we got:

`A=(1)/(2)|108|=54`

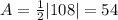
3) Thus the area is 54 square units