Question

Need help with number 10What is the reduced radical form of each expression?

Answer 1

10a²b³

Step-by-step explanation

To simplify this expression, we will use the following properties of exponents:

• Radicals are fractional exponents:

`\sqrt[b]{a}=a^(1/b)`

• Product of powers with the same base:

`a^b\cdot a^c=a^(b+c)`

• Power of a power:

`(a^b)^c=a^(b\cdot c)`

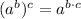
• Exponents can be distributed into the product:

`(a\cdot b)^c=a^c\cdot b^c`

First, write the radicals as fractional exponents,

`\sqrt[]{a^3b^5}\cdot5\sqrt[]{4ab}=(a^3b^5)^(1/2)\cdot5(4ab)^(1/2)`

Distribute the fractional exponents into each product,

`(a^3b^5)^(1/2)\cdot5(4ab)^(1/2)=(a^3)^(1/2)(b^5)^(1/2)\cdot5(4)^(1/2)(a)^(1/2)(b)^(1/2)`

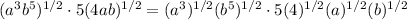
Solve the power of the constants - in this case, the only constant is 4, and also, apply the rule of the power of a power for the first two factors,

`(a^3)^(1/2)(b^5)^(1/2)\cdot5(4)^(1/2)(a)^(1/2)(b)^(1/2)=a^(3/2)\cdot b^(5/2)\cdot5\cdot2\cdot a^(1/2)\cdot b^(1/2)`

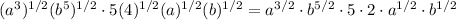
Solve the product between the constants (5*2) and apply the rule of powers with the same base for a and b,

`(a^(3/2)\cdot a^(1/2))\cdot(b^(5/2)\cdot b^(1/2))\cdot(5\cdot2)=(a^(3/2+1/2))\cdot(b^(5/2+1/2))\cdot(10)`

Solve the additions in the exponents and write the constant first,

`(a^(3/2+1/2))\cdot(b^(5/2+1/2))\cdot(10)=10\cdot a^2\cdot b^3`

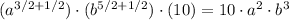
Hence, the simplified expression is 10a²b³ .