Question

14. Factor x4 + 3x2 - 28.O(x2-7)(x - 2)(x + 2)(x2 - 2)(x2 + 14)(x2 + 7)(x-2)(x + 2)O(x² + 4)(x² – 7)

Answer 1

We want to factor the expression;

`x^4+3x^2-28`

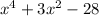
This can by the normal quadratic factorization because the expression even though a

quartic, is quadratic in x^2. Let's simplify it;

`(x^2)^2+3(x^2)-28`

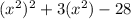
Let us multiply both the constant term and the second power term to obtain

`-28(x^2)^2`

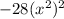
Let us think of numbers that multiply to give this number and also add to give,

`+3x^2`

The two numbers are;

`-4x^2and+7x^2`

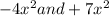
Let's recast the equation then;

`\begin{gathered} (x^2)^2-4x^2+7x^2-28 \\ we\text{ can factorize each pair} \\ x^2(x^2-4)+7(x^2-4) \\ (x^2+7)(x^2-4) \end{gathered}`

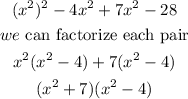
We can factorize one of the terms further as it is a difference of two squares.

`(x^2+7)(x^2-4)=(x^2+7)(x-2)(x+2)`

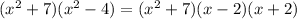
Thus, our final answer is Eoption A