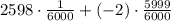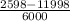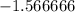Question

In a raffle where 6000 tickets are sold for $2 each, one prize of $2600 will be awarded. What is the expected value of a single ticket in the raffle?

Answer 1

The expeted value of a single ticket is the sum of the value of all probabilities. In this case the probability of winning is:

`(1)/(6000)`

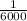
The gain if you win is $2598.

The probability of lossing is:

`(5999)/(6000)`

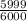
the loss if you lose is $2

The expected value of a single tiket is:

`2598\cdot(1)/(6000)+(-2)\cdot(5999)/(6000)`
`(2598-11998)/(6000)`

`-1.566666`