Question

intercept (Initial value)Depreciation is the decrease or loss in value of an item due to age, wear, or market conditions. We usuallyconsider depreciation on expensive items like cars. Businesses use depreciation as a loss when calculatingtheir income and taxes.One company buys a new bulldozer for $141400. The company depreciates the bulldozer linearly over itsuseful life of 23 years. Its salvage value at the end of 23 years is $11450.A) Express the value of the bulldozer, V, as a function of how many years old it is, t. Make sure to usefunction notation.B) The value of the bulldozer after 17 years is $Question Help: Video Message instructorSubmit Question

Answer 1

A. The first step to solve this question is to find the slope of the linear function, to do it, use the following formula:

`m=(y2-y1)/(x2-x1)`

Replace for the given values, y2 has a value of 141400, y1 a value of 11450, x2 is 0 and x1 a value of 23:

`m=(141400-11450)/(0-23)=-5650`

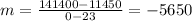
The y intercept is 141400, which is the value of the function when x=0.

Now, we can write the function of the value of the bulldozer in slope intercept form, this way:

`V(t)=-5650t+141400`

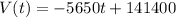
B. To find the value of the bulldozer, replace t for 17 and solve:

`\begin{gathered} V(17)=-5650(17)+141400 \\ V(17)=-96050+141400 \\ V(17)=43350 \end{gathered}`

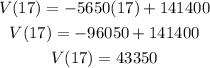
According to this, after 17 years the bulldozer will have a value of $43350.