The given question would form a simultaneous equation.
Let the cost of a movie be "x" and the cost of a video game by "y."
Therefore, when Brian rented 7 movies and 9 video games for a total of $78, this would form this equation.

When Brian rented 5 movies and 3 video games for a total of $36, this would give

To solve the simultaneous equation we need to create equation three and use the elimination method to eliminate one variable.
We would multiply equation two by 3 to get equation three
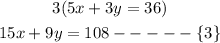
The next step would be to subtract equation two from equation three
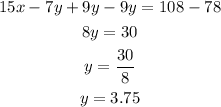
We would then substitute the value of "y" into equation two to get "x."
![undefined]()