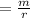We have to simplify the next given expression:
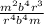
First, we can cancel the common terms b⁴/b⁴ = 1
Then:
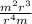
Now, we need to use the next exponents property:
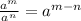
For m:
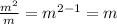
Therefore:

For r:

Use for r the next exponent property:
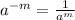
Hence, we have the next simplified expression: