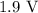Given:
Area = 5.0 cm²
Uniform charges = +8.4 pC or -8.4 pC
Perendicular distance = 1.0 mm
Let's find the potential difference across the metallic plates.
To find the potential difference, apply the formula:
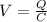
Where:
V is the potential difference
Q is the charge = 8.4 pC
C is the capacitance.
To find C, apply the formula:
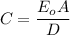
Where:
Eo = 8.85 x 10⁻¹² f/m
A is the area
D is the distance.
Thus, we have:
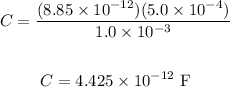
Now, to find the potential difference, we have:
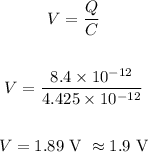
The potential difference across the metallic plates is 1.9 volts
ANSWER: