Given the first three terms of the sequence to be
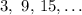
It is observed that each successive term of the sequence is obtained by the addition of 6 to the preceding term.
Thus, the sequence is an arithmetic sequence.
The nth term of an arithmetic sequence is given as
![\begin{gathered} T_n=\text{ a +(n-1)d} \\ \text{where} \\ a\Rightarrow first\text{ term of the sequence} \\ d\Rightarrow common\text{ difference of the sequence, obatined to be the difference betw}een\text{ two consecutive terms of the sequence} \\ n\Rightarrow position\text{ occupied by the term of a sequence} \\ T_n\Rightarrow value\text{ of the nth term of the sequence} \end{gathered}]()
Thus, from the given sequence,
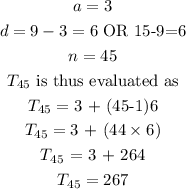
The 45th term of the sequence is thus 267