SOLUTION
looking at the function
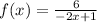
To get the horizontal asymptote, we look at the degree of the numerator and the degree of the denominator.
For the numerator, the degree of the numerator is zero because
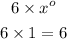
But for the denominator
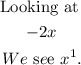
Since the degree of the numerator is less than the degree of the denominator, then the horizontal asymptote is on the x-axis, that is y = 0
To find the vertical asymptote, we set the denominator of the function to be equal to zero. This becomes
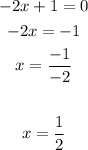
Therefore, the vertical asymptote is
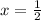
Now, let's do the graph
Below is the graph for the vertical asymptote, horizontal asymptote, and the function
The red line is the horizontal asymptote,
the blue line is the vertical asymptote
the green curve is the function