The given equation is:
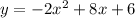
Where x is the acorn's horizontal distance from him and y is the height of the acorn.
We need to solve the equation to find the roots, as follows:
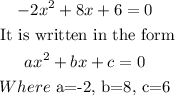
Now,we can apply the quadratic formula to solve for x:
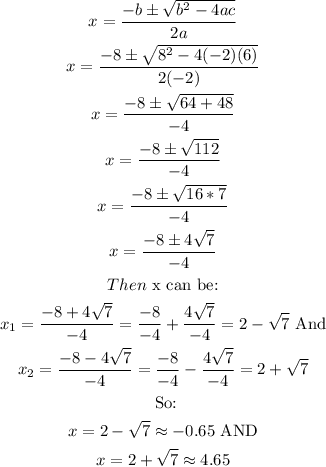
The two solutions for x are -0.65 and 4.65.
The distance can't be negative so x=2-square root(7)=-0.65 feet is not a reasonable solution.
The answer is option D