Question

Let (-5, -2) be a point on the terminal side of 0.Find the exact values of sin , seco, and tan 0.

Answer 1

Notice that if a point (a,b) is on the terminal side of θ, the following triangle is formed:

Remember then, that the length of the hypotenuse of that triangle is given by th Pythagorean Theorem:

`c=\sqrt[]{a^2+b^2}`

Remember also the definitions for sinθ, secθ and tanθ:

`\begin{gathered} \sin \theta=(b)/(c) \\ \sec \theta=(c)/(a) \\ \tan \theta=(b)/(a) \end{gathered}`

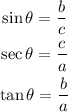
In this case, a=-5 and b=-2. Find c:

`\begin{gathered} c=\sqrt[]{(-5)^2+(-2)^2} \\ =\sqrt[]{25+4} \\ =\sqrt[]{29} \end{gathered}`

Substitute the values for a, b and c to find sinθ, secθ and tanθ:

`\begin{gathered} \sin \theta=-\frac{2}{\sqrt[]{29}}=-\frac{2\cdot\sqrt[]{29}}{29} \\ \sec \theta=-\frac{\sqrt[]{29}}{5} \\ \tan \theta=(-2)/(-5)=(2)/(5) \end{gathered}`

Therefore, the answers are:

`\begin{gathered} \sin \theta=-\frac{2\cdot\sqrt[]{29}}{29} \\ \sec \theta=-\frac{\sqrt[]{29}}{5} \\ \tan \theta=(2)/(5) \end{gathered}`