Question

Find the magnitude of the sun of these two vectors

Answer 1

Given:

Vector A = 63.5 m

Vector B = 101 m at an angle of 57.0 degrees.

Let's find the magnitude of the sum of these two vectors.

To find the magnitude of the sum of the two vector, we have:

Vector A.

X-component and y-component of vector A.

`\begin{gathered} A_x=63.5cos90=0\text{m} \\ \\ A_y=63.5sin90=63.5\text{ m} \end{gathered}`

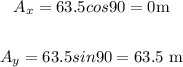
Vector B.

x- and y-component of vector B:

`\begin{gathered} B_x=101cos57=55\text{ m} \\ \\ B_y=101sin57=84.7\text{ m} \end{gathered}`

Now, to find the magnitude of the sum of the vectors, we have:

`\begin{gathered} √((A_x+B_x)^2+(A_y+B_y)^2) \\ \\ √((0+55)^2+(63.5+84.7)^2) \end{gathered}`

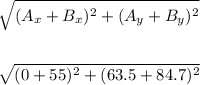
Solving further:

`\begin{gathered} √(3025+(148.2)^2) \\ \\ √(3025+21963.24) \\ \\ √(24988.24) \\ \\ =158.08\text{ m} \end{gathered}`

Therefore, the magnitude of the sum of these two vectors is 158.08 m.

ANSWER: