Given:
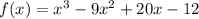
For y intercept the value of x=0
then :
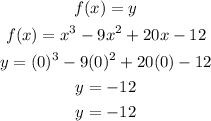
so y -intercept is -12.
For x intercept the value of y is zero.
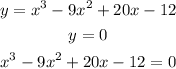
If one factor is (x-6) then other factor is:
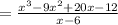
So all factor is:
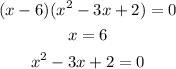
one x intercept 6 and another intercept is:
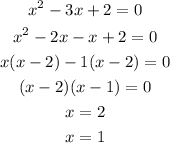
So x - intercept of graph is
1,2,6